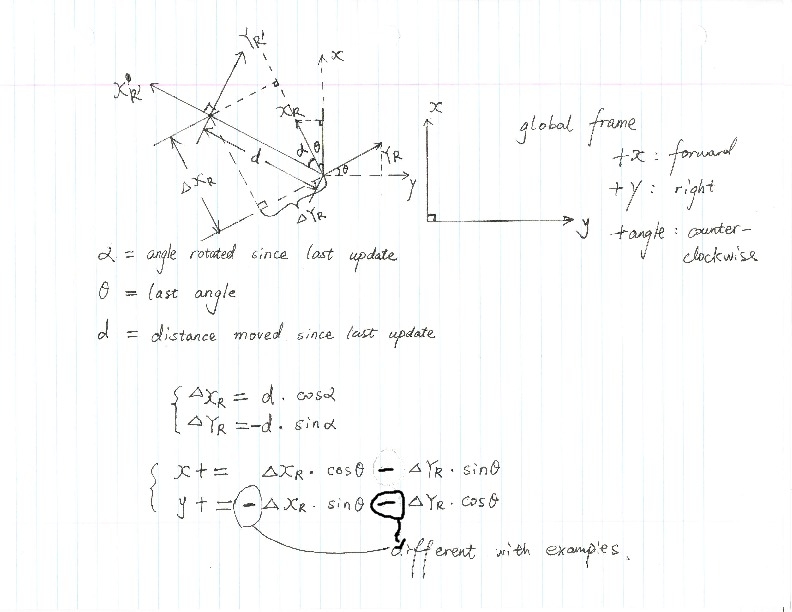
how to calculate the odometry for irobot create robot

edit

Hi,

I'm trying to understand how the odometry is calculated in irobot_create_2_1 driver. I spent lots of time trying to figure out where the minus sign comes from in y=-sin(th)*d, on the 53th line in driver.py. I've included the code snippet. I also included the odometry calculation part in turtlebot_node.py from turtlebot stack, which does the same thing but easier for me to understand.

Can anyone give me a hint or let me know where I can find good resource on mobile robot odometry/kinematics in order to understand the whole scenario. Thanks

From driver.py

00046                 d = self.create.d_distance / 1000.
00047                 th = self.create.d_angle*pi/180
00048                 dx = d / elapsed
00049                 dth = th / elapsed
00050 
00051                 if (d != 0):
00052                         x = cos(th)*d
00053                         y = -sin(th)*d
00054                         self.x = self.x + (cos(self.th)*x - sin(self.th)*y)
00055                         self.y = self.y + (sin(self.th)*x + cos(self.th)*y)
00056 
00057                 if (th != 0):
00058                         self.th = self.th + th

From turtlebot_node.py

    # this is really delta_distance, delta_angle
    d  = sensor_state.distance * self.odom_linear_scale_correction #correction factor from calibration
    angle = sensor_state.angle * self.odom_angular_scale_correction #correction factor from calibration

    x = cos(angle) * d
    y = -sin(angle) * d

    last_angle = self._pos2d.theta
    self._pos2d.x += cos(last_angle)*x - sin(last_angle)*y
    self._pos2d.y += sin(last_angle)*x + cos(last_angle)*y
    self._pos2d.theta += angle

I've attached my calculation as below, can someone point out where went wrong?