Using laser_scan_matcher output

edit

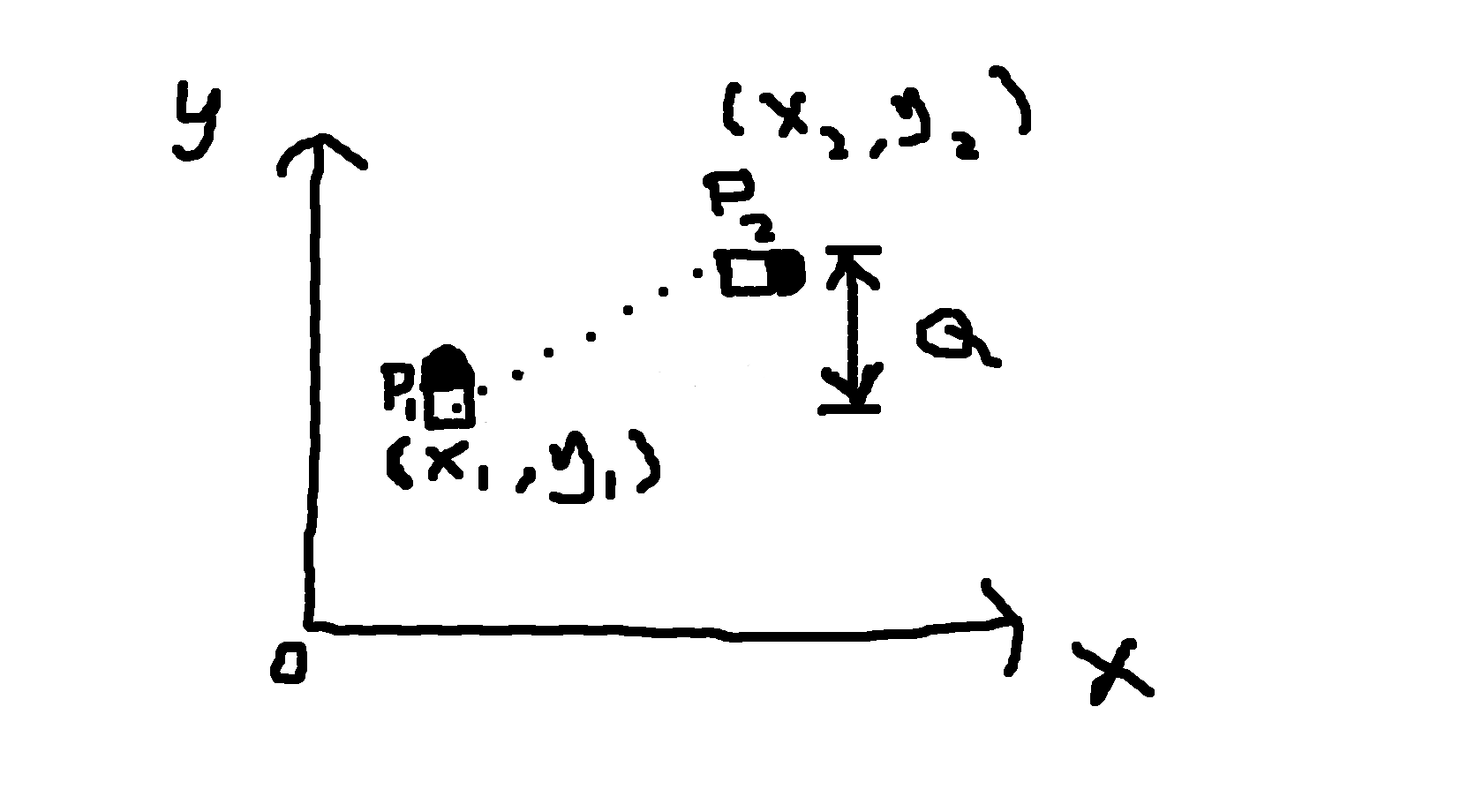
I would like to have a confirmation on my understanding in order to use the output of laser_scan_matcher(lsm) in a correct way. Kindly refer to the provided figure(sorry for providing a mere sketch). For convention, please assume any subscript of 1 refers to the previous data(means x1= previous x value from lsm and so on). Likewise, subscript of 2 refers to the current data. P1 and P2 is the position of the x and y values returned by pose2D of the previous and current values respectively that have been mapped into a cartesian coordinate.

My questions are:

1. Is that correct the representation of variables in the context of lsm?

2. Calculation of Q:

   i) Either:

   Q = sqrt[(x2-x1)² + (y2-y1)²] x sin(theta1)  OR 
   Q = sqrt[(x2-x1)² + (y2-y1)²] x sin(theta2) OR
   Q = sqrt[(x2-x1)² + (y2-y1)²] x sin(theta2-theta1)
   

   ii) OR Q = x2-x1

This sounds like a fundamental math problem, but with respect to the values returned by lsm makes me confused. Perhaps someone who is experienced using the package or preferably the author himself can give some comments regarding this.

In my opinion, the correct one should be Q = sqrt[(x2-x1)² + (y2-y1)²] x sin(theta1), but I don't know if this one is correct or not in this regard.

Thanks in advance.

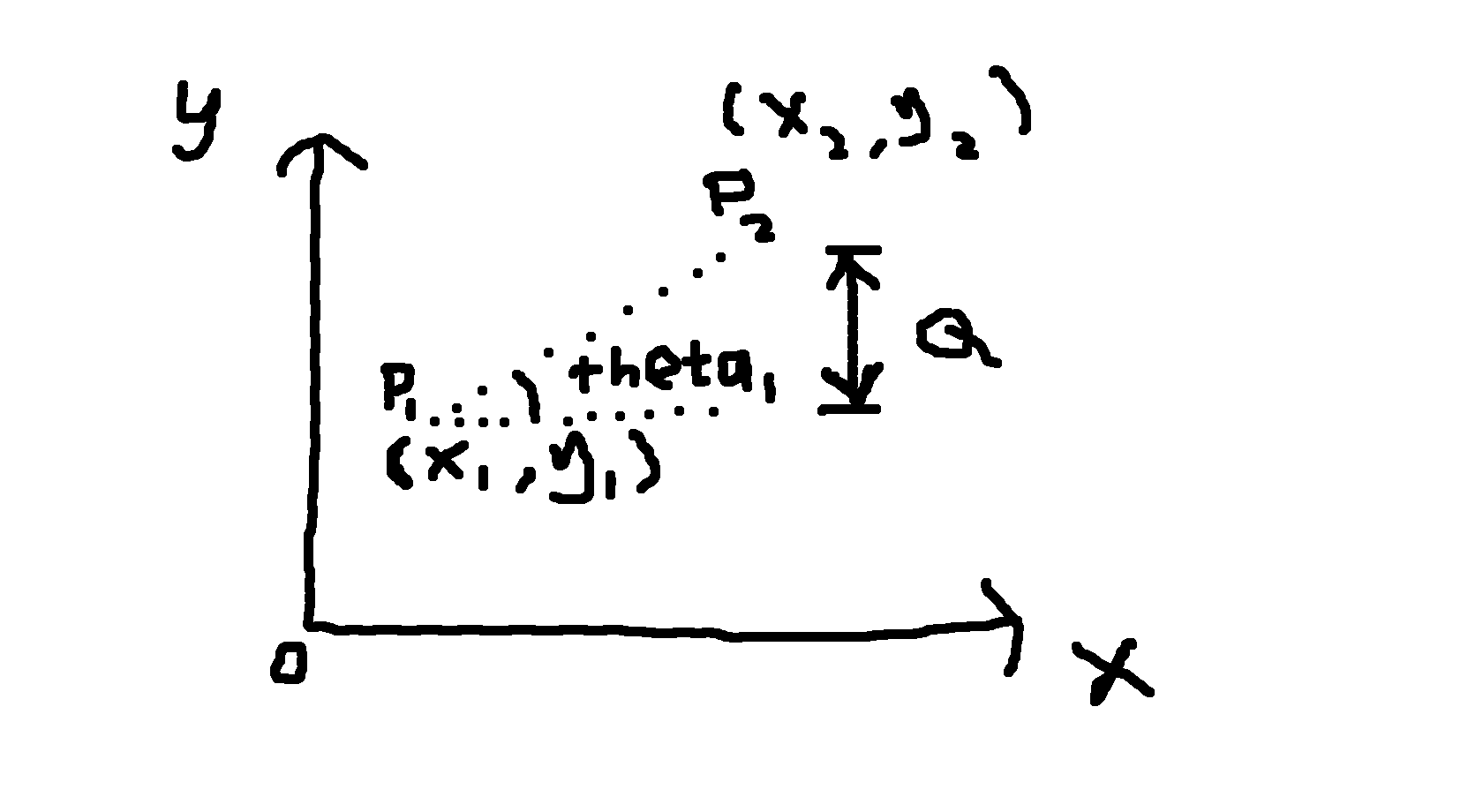
EDIT: