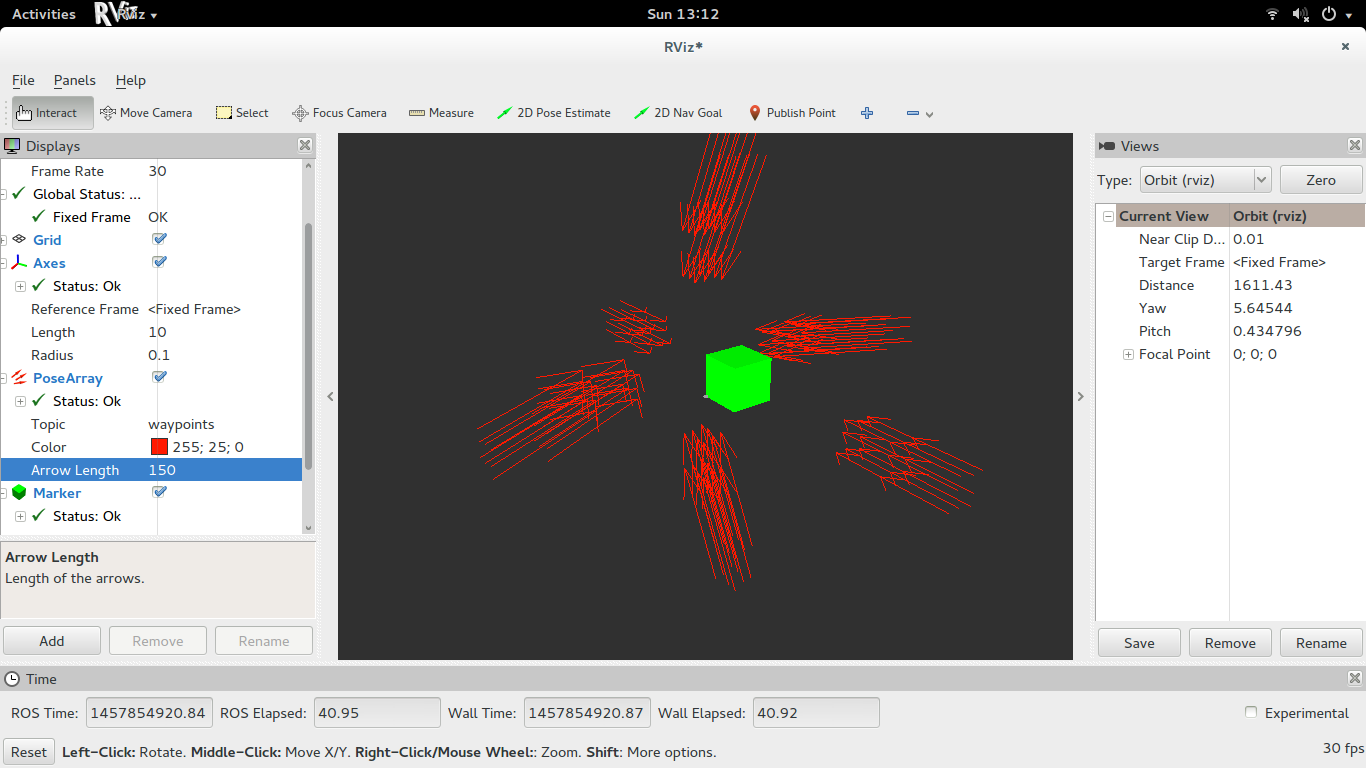
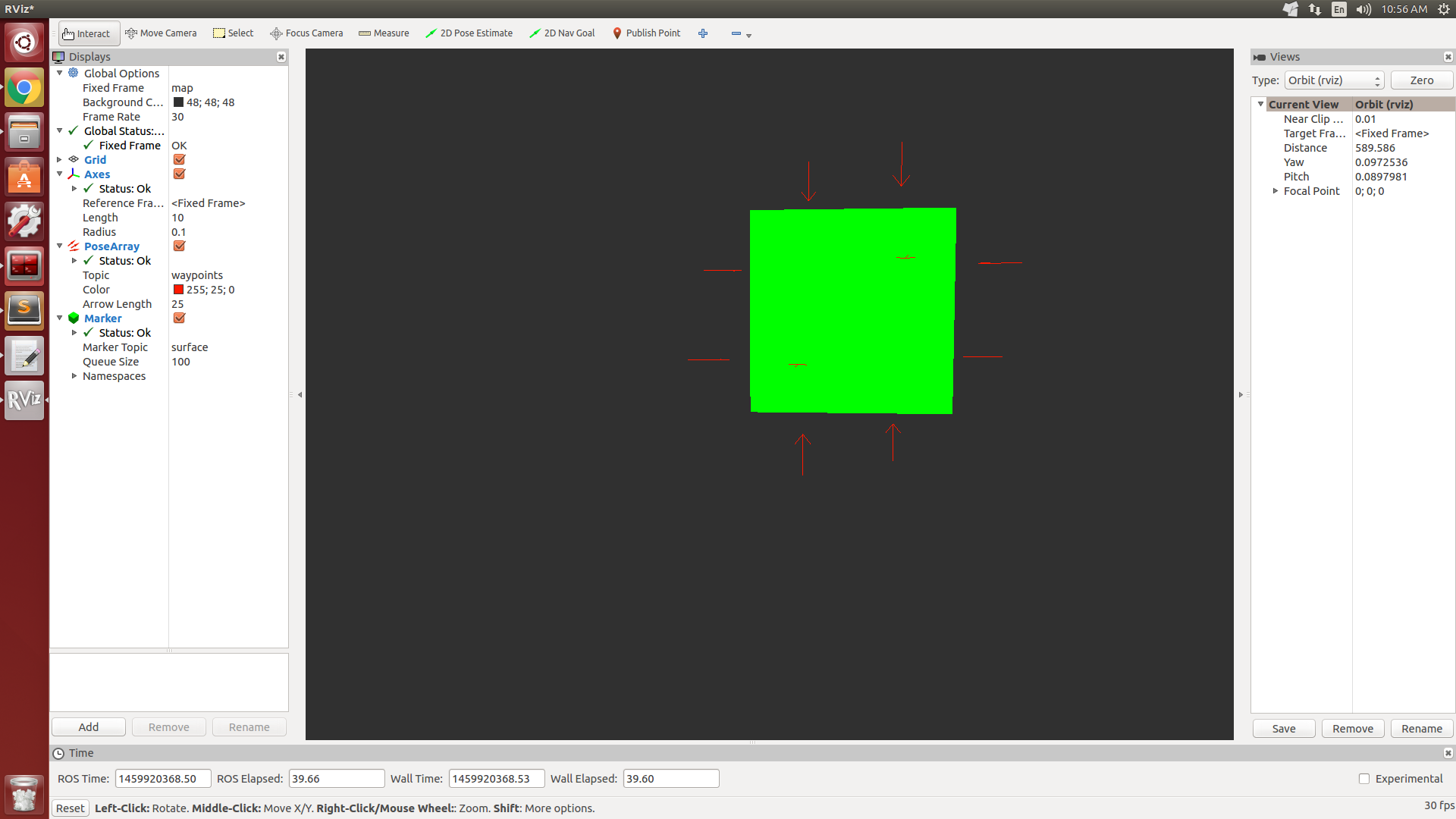
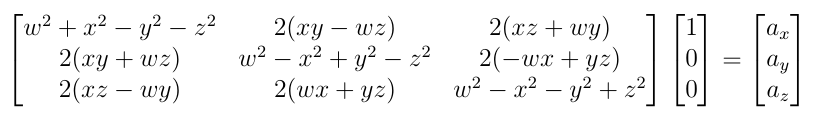Technically, no unique quaternion can represent an arbitrary 3D vector. Assuming the vector represents the x axis of the transformed frame, you're essentially solving the following equation for the quaternion parameters given your vector [a_x, a_y, a_z]
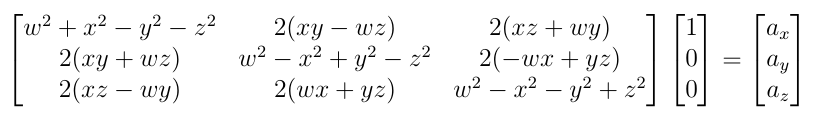
From this, it is clear that there is no unique solution, simply because there are four unknowns (the quaternion parameters), and only three independent equations. This can be verified intuitively as well. Imagine the x axis of a frame aligned along a particular orientation. The roll angle around that x axis is arbitrary, as it doesn't affect the orientation of the x axis relative to the base frame.
Therefore, the solution needs to be constrained in some way. One way is to constrain the y axis to be in a level plane w.r.t. the base frame (z = 0). Here is some code that I wrote using the Eigen library to construct a rotation matrix out of basis vectors that define the orientation of a vector. It assumes you have a using namespace Eigen; in your source file.
Vector3d u1, u2, u3;
Vector3d a;
a << 1, 2, 3; // Some arbitrary vector
u1 = a.normalized();
if ((fabs((double)u1(0)) > 0.001) || (fabs((double)u1(1)) > 0.001)) {
u2 << -u1(1), u1(0), 0;
} else {
u2 << 0, u1(2), -u1(1);
}
u2.normalize();
u3 = u1.cross(u2);
Matrix3d R; // Rotation matrix defining orientation
R.col(0) = u1;
R.col(1) = u2;
R.col(2) = u3;
There are algorithms to convert a rotation matrix to a quaternion. Probably the simplest way to do this is to use a tf::Transform. First, convert the Eigen::Matrix3d to a tf::Matrix3x3 and call the setBasis() method of the tf::Transform. Then call the getRotation() method to get a tf::Quaternion with the parameters.
I hope this helps!